
Calculus Without Tears
The Wave Equation
Introduction
In the CWT texts we analyze motion problems using Newton's Second Law, and electrical circuits using the differential equations that characterize electrical components along with the relevant circuit laws. In this page we will see how the techniques we have studied can be applied to analyze wave motion.
The basic physics/engineering paradigm is: start by analyzing the system and writing the differential equations that characterize it, then solve the differential equations, so that's what we'll do. We'll see that the wave equation can be derived from physical principles we've already studied plus the ideal gas law.
Calculus with Multiple Variables
For simplicities sake, CWT only deals with functions of one variable. We can't represent a wave whose amplitude changes with position and time with a function of just one variable, as we need variables to represent both position and time. Waves occur in 3-dimensional space, and it takes 3 numbers to represent a position in 3-dimensional space, so we can represent an acoustic wave with a function p(x,y,z,t) where x,y, and z are spatial coordinates and t is time, and p(x,y,z,t) is the displacement from the equilibrium pressure at the point x, y, z at time t.
By considering one dimensional waves we will be able to limit ourselves to functions of two variables in what follows. Below we will use a two variable function p(x,t) where x is a location variable and t is time. When we have functions of more than one variable, derivatives are called 'partial derivatives'. For example the function v below is a function of two variables, x and t,
v(x,t) = 3*x2 + x*t2
By considering x to be a constant the function becomes a polynomial with one variable, t, and we can differentiate it wrt t, and the result is called the partial derivative of v wrt t and is denoted by 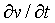 , that is
, that is 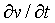 is the name of the derivative, and
is the name of the derivative, and
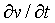 (x,t) = x*2*t,
(x,t) = x*2*t,
(remember, x is constant so 3*x2 is a constant and has derivative 0, and the derivative of x*t2 wrt t is x*2*t).
Similarly, by considering t to be a constant we can differentiate the function wrt x to get the partial derivative of v wrt x, given by
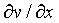 (x,t) = 6*x + t2
(x,t) = 6*x + t2
We can take 2nd order partial derivatives
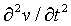 =
= 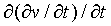 =
= 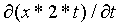 = x*2
= x*2
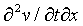 =
= 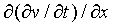 =
= 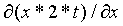 = 2*t
= 2*t
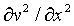 =
= 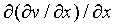 =
= 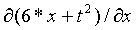 = 6
= 6
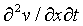 =
= 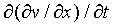 =
= 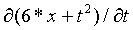 = 2*t
= 2*t
Note that
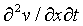 =
= 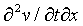
We will use this important property of partial derivatives on this page and on the general relativity page.
Also, note that 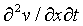 is just the name of a function, (we could have named the function "Fred" if we were inclined to defy convention), that is obtained by first taking the partial derivative of v wrt t and then taking the partial derivative of that function wrt x. We have introduced a fancy notation, but the concept of derivative hasn't changed at all, it is identical to what is covered in CWT Vol. 2. The
is just the name of a function, (we could have named the function "Fred" if we were inclined to defy convention), that is obtained by first taking the partial derivative of v wrt t and then taking the partial derivative of that function wrt x. We have introduced a fancy notation, but the concept of derivative hasn't changed at all, it is identical to what is covered in CWT Vol. 2. The 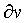 s and
s and 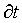 s have no intrinisic meaning, they are just used to write the conventional names for partial derivative functions.
s have no intrinisic meaning, they are just used to write the conventional names for partial derivative functions.
The Wave Equation
The wave equation characterizes wave motion in gas, liquids, and solids, as well as electromagnetic waves. We'll examine the acoustic case, this equation describes how sound waves propagate in air.
We will show one derivation of the wave equation in this section, and another in the section on Maxwell's equations.
A Derivation of the Acoustic Wave Equation
The Ideal Gas Law
We will need the ideal gas law from chemistry which is P · V = m · R · T, where
P = pressure
V = volume
m = mass
R = the universal gas constant = 287 J·kg-1·K-1
T = temperature in degrees Kelvin, T = C + 273.15 where C is temperature in degrees Celcius
The ideal gas law says that (at a fixed temperature) the pressure of the gas in a fixed volume is directly proportional to the mass of the gas, that is, as the mass increases the pressure increases, and as the mass decreases the pressure decreases. As you pump air into the tire the pressure increases, as you let air out it decreases. No big surprise.
A One Dimensional Physical Model
We'll limit the number of spatial dimensions to 1 by assuming that we have a very small straight hollow tube filled with air, and that the air moves only in the direction of the tube. We will study the motion and the pressure of air in the tube.
The constant P will represent the equilibrium pressure, that is, atmospheric pressure. The function p(x,t) will represent the displacement from the equilibrium pressure due to an acoustic wave at location x at time t.
The function v(x,t) will represent the velocity of the air in the tube at location x at time t. When no wave is present v(x,t) = 0 for all x.
The Acceleration of Air in the Tube
The image below represents a thin hollow tube filled with air. The x variable measures position along the length of the tube.
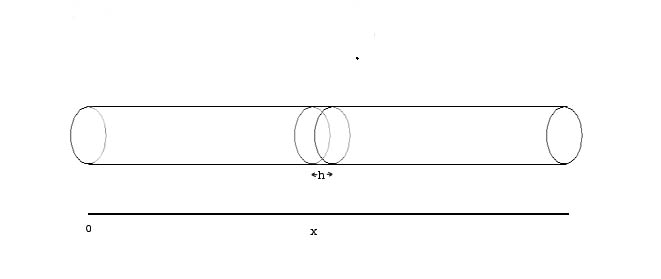 The cross sectional area of the tube is A and is very small.
The cross sectional area of the tube is A and is very small.
The volume of the air in the tube segment between x and x+h is Vs = A*h.
Consider the forces acting on the air in this segment
time t. From the left, the force equals p(x,t) ·A, and from the right the force is p(x+h,t) ·A (note that the forces due to P cancel).
So the total force is [p(x,t) - p(x+h,t)] ·A.
From Newton's 2nd Law of Motion F = m ·Acceleration, so, the acceleration of the air between x and x+h is given by F / m, that is,
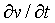 = [p(x,t) - p(x+h,t)]·A / ms
= [p(x,t) - p(x+h,t)]·A / ms
From the ideal gas law we have ms = P·Vs / R·T, so
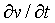 = [p(x,t) - p(x+h,t)] ·A · R · T / P · Vs
= [p(x,t) - p(x+h,t)] ·A · R · T / P · Vs
Note that A / Vs equals 1/h, so, as h -> 0 the above equation becomes
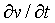 = -
= - 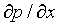 · R·T / P
· R·T / P
That is, a spatial pressure 'differential' causes the air in the tube to accelerate.
The Time Derivative of Pressure
Air flows into the left side of the segment at x to x+h at the rate v(x,t)·A and flows out the right side at the rate v(x+h,t)·A. Thus
the total rate of the the air flowing into the segment is
[v(x,t) - v(x+h,t)] ·A
This will produce a change in the pressure in the segment. First we convert the volume rate to a mass rate. From the ideal gas law the density of the
air is m / V = P / R·T , so the mass rate into the segment is
[v(x,t) - v(x+h,t)] ·A·P / R·T
Now we will convert the mass rate into a pressure rate. From the ideal gas law, the ratio of pressure to mass in the segment is R·T / Vs, so we have
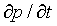 = [v(x,t) - v(x+h,t)] ·A·P / R·T · [R·T / Vs] = [v(x,t) - v(x+h,t)] ·A·P / Vs
= [v(x,t) - v(x+h,t)] ·A·P / R·T · [R·T / Vs] = [v(x,t) - v(x+h,t)] ·A·P / Vs
Note that A / Vs is 1/h. As h -> 0, the above equation becomes
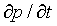 = -
= - 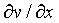 · P
· P
That is, a spatial velocity 'differential' causes pressure to increase or decrease.
The Second Time Derivative of Pressure
Taking the second partial derivative of pressure wrt time gives
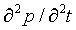 = -
= - 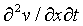 · P
· P
Taking the partial derivative of acceleration wrt x gives
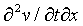 = -
= - 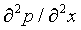 · R·T / P
· R·T / P
Noting that 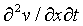 =
= 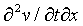 and substituting gives the wave equation
and substituting gives the wave equation
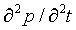 =
= 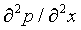 · R·T
· R·T
The Speed of Sound
It is easy to check by differentiating that the solution to the wave equation
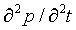 = (w / k)2 ·
= (w / k)2 · 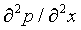
is
p(t,x) = p0 cos(kx - wt)
The velocity of wave propagation is the spatial length of a stationary wave, 2π/k, times the number of waves that pass by per second, w/2π, that is, w/k. So, the speed of sound in air is calculated by setting
(w/k)2 = R·T
and calculating the speed of sound (at 30 deg. C) by,
w/k = sqrt(R·T) = sqrt(287·303.15) = 295 m/s