Calculus Without Tears

Relativity

Introduction

Although the theory of special relativity, proposed by Einstein in 1905, doesn't depend on calculus, there are several good reasons for including a discussion of it here. Not the least of which is it gets us, just barely, into the twentieth century (note: twentieth, not twentyfirst). It followed from studies of Maxwell's equations. It reshaped the Newtonian physics we have studied. It explains magnetism - this is the coolest thing! And, it is a necessary preliminary to general relativity.

As for math, all you need is the Pythagorean theorem! No kidding.

Space, Time, and Inertial Coordinate Systems, According to Galileo

Our notions of space and time date originated with the Greeks and in particular Euclid's geometry. However, not much was made of these concepts until Decartes invented 'cartesian coordinates' and the rapid development in physics that began in the 17th century. 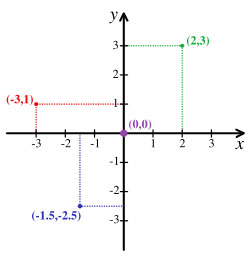Two dimensional cartesian coordinates are shown to the left. Another axis, the 'z' axis, is added to make a three dimensional coordinate system. In physics, positions, velocities, etc., are specified as coordinates in a specific three dimensional coordinate system.

The laws of physics, e.g. F=M*A, relate the measurements made in a particular coordinate system. Can we use just any coordinate system? The answer is no; intuitively, we would like for the axes, also called the frame, to be stable. The most stable frame would be one that is 'fixed' in space, however, the concept of a frame fixed in space is impossible to pin down. Galileo settled on the idea of a frame that is moving uniformly, that is, moving at a constant velocity and neither accelerating or turning. Galileo called such coordinate frames 'inertial', and formulated the first principle of relativity, stating that the laws of physics should hold for measurements made in (i.e. relative to) any inertial coordinate frame.

Finding an inertial frame can be a bit daunting. Let's suppose we're on an airplane. Airplane applications use a frame with its origin at the airplane's center of gravity, with the x axis pointing straight ahead (this is the roll axis), the y axis pointing out the left wing (this is the pitch axis), and the z axis pointing up (this is the yaw axis). Measurements made by sensors on the aircraft, e.g. gyros, accelerometers, radar, are necessarily made in this frame. However, the origin of the frame can accelerate, and the frame can turn; clearly it is not inertial, and Newton's laws do not apply to measurements made in this frame. OK, the airplane was a bad place to start, let's try something on the ground. A commonly used frame is ENU coordinates, with the origin located at a fixed location on earth, and the axes pointing east(E), north(N), and up(U). Are ENU coordinates truly inertial? No, since the earth is rotating, the origin is moving and the frame is turning (however, it is a close enough approximation to an inertial frame for the analysis of small scale local phenomena). Trying for more stablity still engineers use ECI (earth centered inertial) coordinates, with the origin at the center of the earth, with the z axis along the earth's axis of rotation, and the x axis aligned with the Greenwich meridian at some specified instant (and then fixed in space). Since the origin of this frame is circling the sun, it is also not truly inertial. Sun centered inertial coordinates (SCI) might do the trick, but note that SCI coordinates are unusable for the analysis of phenomena on the earth (the numbers are too big and changing too rapidly).

The Galilean Coordinate Transformation

Let's leave our search for a true inertial frame to consider another problem addressed by Galileo. How do the measurements in one inertial frame relate to those in another? Suppose the axes of inertial frames O and O' are aligned, and that their origins coincide at time t = 0. Suppose that frame O' is moving in frame O with fixed velocity v in the direction of the x (and x') axis.

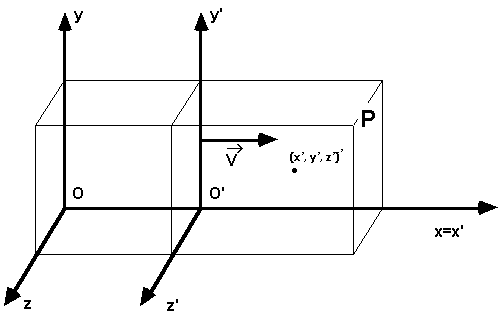
How can we convert coordinates measured in frame O' at time t to the appropriate values in frame O? Well, at time t the location of the origin for O' is (vt, 0, 0) in O frame coordinates. It is easy to see that a point with coordinates (x', y', z')' in frame O' will have coordinates (x' + vt, y', z') in frame O, so the coordinate transform is given by
x = x' + vt
y = y'
z = z'

Note: we'll write (-,-,-) for O frame coordinates of a point, and (-,-,-)' for O' coordinates of a point.

Let u'=(u_x', u_y', u_z') be the velocity of a particle measured in O' coordinates, it is clear that the velocities transfrom
u_x = u_x' + v
u_y = u_y'
u_z = u_z'
and that accelerations transform
a_x = a_x'
a_y = a_y'
a_z = v_z'

This is the Galilean coordinate transformation. It is just the formalization of the notions of time and space that had existed since Euclid.

In what follows we will need to think of 'events' ... like a flash going off. An event has spatial coordinates and a time coordinate, thus we need four coordinates to locate an event in time and space, which we will designate by (t, x, y, z). If t' is the time coordinate of an event in the O' frame, and t the time coordinate of the same event in the O frame, it was obvious to all and sundry that t = t'.

Galileo's Theory of Relativity

Galileo formulated his principles of relativity, which state:
1 - the laws of physics can be applied to the measurements made relative to (i.e. in) any inertial frame, and they will produce correct results, and
2 - the correspondence between the coordinates in one inertial frame and the coordinates in another inertial frame is given by the Galilean coordinate transformation

Einstein's Theory of Special Relativity

The theory of special relativity proposed by Einstein states:
1 - same as 1 in Galileo's theory
2 - the speed of light is the same in all inertial frames,
3 - the correspondence between the coordinates in one inertial frame and the coordinates in another inertial frame is given by the Lorentz coordinate transformation

So, three questions need to be answered, first, why do we believe the speed of light is the same in all inertial frames, second, what problems caused scientists to doubt the Galilean coordinate tranformation, and third, what is the Lorentz coordinate transformation and how does it solve those problems.

The Michelson Morley Experiment

As we have seen, Maxwell's equations can be used to derive a wave equation and predict the speed of light = c. But, in what frame? Consider sound; the acoustic wave equation (same wave equation, different constant) predicts the speed of sound. Well, in what frame? In an inertial frame in which the air is stationary. So, it was hypothesized that there was an 'ether' that served as a carrier for electromagnetic radiation just as air is a carrier of sound waves. If light is vibrations in the ether, then its speed would be c in an inertial frame in which the ether is stationary, and its speed in other inertial frames could be calculated using the Galilean coordinate transformation. Where is this ether? Everywhere, because electromagnetic radiation is observed everywhere. An inertial frame in which the ether is stationary would constitute the 'mother of all inertial frames'.

Michelson and Morley 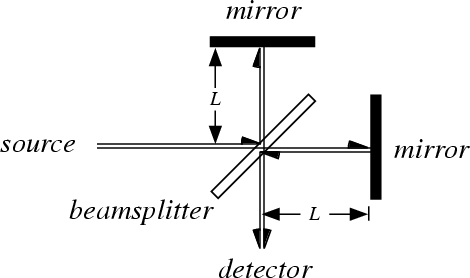designed an experiment to detect the ether and measure its influence on the speed of light. They reasoned that if they put their apparatus on the top of a mountain, then the apparatus would be zipping through the ether at a high rate of speed, and they would be able to detect it with a clever experiment. They calculated that if they launched a beam of light in the direction of their velocity through the ether, reflected it off a mirror, and timed its return, then that time would differ from the return time if they launched the beam perpendicular to the direction of motion through the ether. The difference in return times would confirm the presence of the ether. Instead, their results showed that the speed of light was the same regardless of direction. Thus the hypothesis of the ether was rejected.

Let's do the math. Assume light travels at a constant velocity c in the ether. Suppose the apparatus is moving through the stationary ether with velocity v. In the direction of motion, the time for the light to reach the mirror and come back is T = L/(c - v) + L/(c + v). In the direction perpendicular to the motion, the time to reach the mirror and come back is calculated by solving (cT)² = L² + (vT)², so T = (L² / (c² - v²))^1/2 (see diagram in time dilation section below - same calculation). The experimental results did not match these calculations. Instead T was the same for both directions (T = 2L/c ).

The conclusion of the Michelson-Morley experiment was that the speed of light was a constant c in any inertial frame. Why is this result so surprising? First, it invalidates the Galilean coordinate transformation. Note that with the frames as defined in the previous section, if light is travelling in the x' direction in frame O' with velocity c, then its speed in the O frame is, by the Galilean transform, c + v, not c as measured. This invalidates two thousand years of understanding of the nature of time and space.

The only comparable discovery is the discovery that the earth isn't flat! The Michelson Morley experiment has inevitably brought about a profound change in our understanding of the world.

A Mystery, and a Hint

Suppose, as above, the O' frame is moving with fixed velocity v in the O frame. And suppose at time t = t' = 0 the origins of the O frame and the O' frame coincide, and a light flashes at the origin of both frames. The velocity of light is c in the O frame so to an observer in the O frame it appears to expand outward in a ball of radius ct, centered at (0,0,0) in the O frame. The velocity of light is also c in the O' frame, so, to an observer in the O' frame it appears to expand outward in a ball of radius ct' centered at (0, 0, 0)' in the O' frame. But, (0, 0, 0)' in the O' frame is at location (vt, 0, 0) in the O frame.

So, where is the center of the expanding ball of light at time t? At (0, 0, 0) in the O frame, or (0, 0, 0)' in the O' frame, i.e. (vt, 0, 0) in the O frame.

Here is a hint - at an instant t in the O frame, the light appears to be a ball centered at (0, 0, 0) in the O frame. Similarly, at an instant t' in the O' frame, the light appears to be a ball centered at (0, 0, 0)' in the O' frame. We naturally assume that an instant in the O frame corresponds to an instant in the O' frame. That is, that events that are simultaneous in one frame are simultaneous in any other frame. Perhaps this assumption is not warranted.

This mystery has a solution, which is presented below (A Mystery Solved). To solve it, we will have to think carefully and we will have to be very explicit about observers, times, instants, places, and events.

Time Dilation

Einstein's special theory of relativity is all a direct consequence of two easy thought experiments showing time dilation and length contraction. So this section and the next contain the crux of the theory.

First, we design a perfect clock. 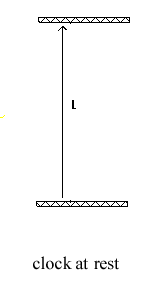Two mirrors are located at a distance L apart, facing each other. At time t = 0 a light is flashed on the lower mirror. The light travels a distance L to the upper mirror, and then in reflected back to the lower mirror. Each trip from mirror to mirror counts as one tick of the clock. The time for one tick is L/c.

Now, we'll use our clock in a little experiment. Suppose the clock is in frame O' that is moving to the right in frame O with velocity v. What does an observer in frame O see. As the light leaves the bottom mirror, it and the mirror are observed to be travelling to the right with velocity v. Suppose the light takes 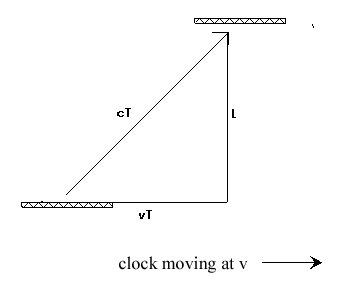time T to reach the top mirror. Then both mirrors will have travelled to the right the distance vT, and distance the light will have travelled as observed by O, is cT, and, by the Pythagorean theorem
(cT)² = (vT)² + L²
so, T²(c² - v²) = L²
T² = L² / (c² - v²)
T² = L² / c²(1 - v²/c²))
T = L/c (1/)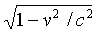
The expression (1/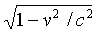) occurs frequently in relativity and is designated by the symbol γ, that is
γ = (1/)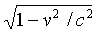
So, one tick of the clock in frame O' appears to take γ ticks in frame O. An observer in frame O will conclude that the clock in frame O' is running slow, since γ > 1. This phenomena is referred to as time dilation. It means that as observed from the O frame, the clock appears to have slowed down. To an observer in the O frame, time is passing more slowly in the O' frame.

Summarizing, T = T'γ

Length Contraction

Note: in the clock above the mirrors were oriented so that the distance between them (L) was measured perpendicular to the velocity vector v. Distance perpendicular to v will be measured the same in frame O and O'. However, distances in the direction of v will measure shorter in frame O than they measure in frame O'. That phenomena is called length contraction. We turn our attention to it.

Suppose that the length of a stationary rod in the O' frame is determined by putting a mirror at one end, flashing a light at the other end, and measuring how long the light takes to travel to the end of the rod and be reflected back. If that time is T' then the length of the rod L' is cT'/2.

Suppose that the O and O' frames are aligned, that the O' frame is moving to the right with velocity v, that their origins coincide at t = t' = 0, and that the light at the left end of rod flashes at time t = t' = 0. 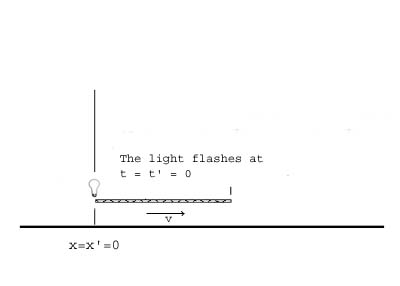We will need to modify our procedure to calculate the length in the O frame.
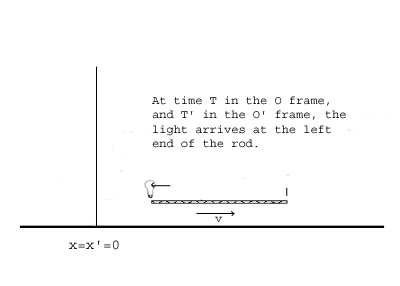
Suppose an observer in the O frame sees the light bounce off the mirror at the right end of the rod and reach the left end at time T. Let L be the measured length of the rod in the O frame. The time for the light to travel from left end of the rod to the right end is L/(c - v) and the time for the light to come back from the right end to the left is L/(c + v), thus
T = L/(c - v) + L/(c + v) = 2cL/(c² - v²) = 2L/c(1 - v²/c²) = 2L/c γ²
Suppose that there was a O' frame clock attached to the left end of the rod, and that this clock reads T' when the light reaches the left end of the rod. Because of time dilation, we know that
T = T'γ = 2L'/cγ
so, L = L' / γ
Thus an object that has length L' in the x direction in the O' frame will appear to have length L = L' / γ in the O frame. This phenomenon is known as length contraction.

Summarizing, L = L' / γ

Simultaneity, the Now Line, and Space-Time Diagrams

We're on our way to the Lorentz coordinate transformation, but, we want to slow down and draw some pictures.

Space-time Diagrams

First, we will always assume that the axes of the O and O' frames are aligned, and we will assume that the motion of O' is in the x direction with velocity v. With these assumptions, the Lorentz transformation for the y' and z' coordinates is identical to the Galilean transformation, that is, y = y' and z = z'. So, we'll not worry with these axes and only worry about transforming the x and t coordinates. We can represent the (t, x) space-time with a two dimensional graph.

Also, c, the speed of light is a constant, and if we scale x appropriately, that is in units of light-seconds, then the value of c is 1. We will do this. With this scaling γ = 1/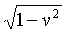

We will plot t along the horizontal axis and x along the vertical axis in our space-time diagrams. The point with coordinates (t, x) represents the location of the event occuring at time t and location x. As an object exists, its (x, t) coordinates constitute a worldline than can be plotted on a space-time diagram.

A space-time diagram for an observer in the O frame is shown. 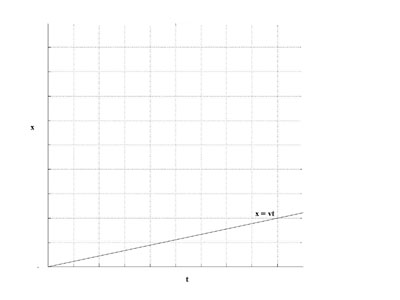Suppose the O' frame is aligned with the O frame, and the origins of the frames coincide at time t = t' = 0, and that the O' frame is moving with velocity v in the x direction in the O frame. The worldline for the origin of the O' frame is shown in the diagram.

Space-time Diagrams for O and O' Showing the Galilean Coordinate Transformation

Now, to get our feet on the ground, we will show a Galilean coordinate transformation graphically. That is, we will draw the O' space-time diagram on top of the O space-time diagram. 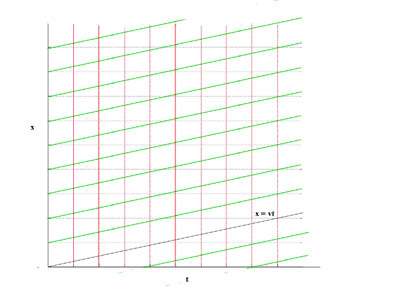We will draw the space-time diagram for O' at time t' = 0. First, which points on the diagram above correspond to the x' = 0 line in the O' space-time diagram?

In the O frame, the horizontal black lines of the rectangular grid are worldlines of stationary objects at locations x= 0, x = 1, x = 2, etc. The vertical lines of the grid are now lines for t = 0, t = 1, t = 2, etc.

The x' = 0 line is the worldline of the origin of the O' frame (green in the diagram). The x' = 1 , 2, 3, etc. lines are parallel to this line as shown. The spacing of the x' lines is the same as the spacing of the x lines. The t' = 0, 1, 2, 3, etc. lines are the same as the t = 0, 1, 2, 3, etc., lines in the O frame.

The now lines in the O' frame are red. For a Galilean coordinate transfomation, the now lines are the same in both frames, hence the O and O' frame now lines coincide.

We can use the composite diagram to determine the coordinates of a point in either frame by projecting it onto the appropriate axes.

Space-time Diagrams for the Lorentz Coordinate Transformation - The O' Worldline

The Lorentz coordinate transfromation incorporates time dilation and length contraction, so we will need to account for these effects when plotting the O' space-time diagram. However, the x' = 0 axis of the O' frame still lies along the world line for the O' frame origin, so it will appear as above. Let's calculate the O frame coordinates (t, x) of the point (t', 0)' on the x' = 0 line in the O' frame. The clock at x' = 0 in the O' frame was synchronized with the clock at x = 0 in the O frame at time t = t' = 0, so, when the clock on the x' = 0 line reads t', the O frame clock at x = 0 reads t'γ due to time dilation. So, t = t'γ; the equation for the x' = 0 line is x = vt, so the x coordinate is t'γv.

Summarizing, the O frame coordinates of (t', 0)' are ( t'γ, t'γv) .

A Now Line Experiment

How about the t' = 0 line in the O' frame. This is the 'now line' for O'. This line represent the instant in the O' frame at time t' = 0. We will do an experiment to get the coordinates of this line in terms of t and x in the O frame. Imagine that a rod of length L' in the O' frame is moving to the right with velocity v in the O frame so that its left end will arrive at x'=0 at time t'=0. A light placed in the center of the rod flashes just so that the light reaches the ends of the rod at t'=0 in the O' frame.

An observer in the O frame sees the light flash at the middle of a rod of length L and reach the left end of the rod at time t = 0. How long did this light travel in the O frame? Ans: L/2(1 + v). It arrives at time t = 0. The observer also sees the light travel from the flash to the right end of the rod. 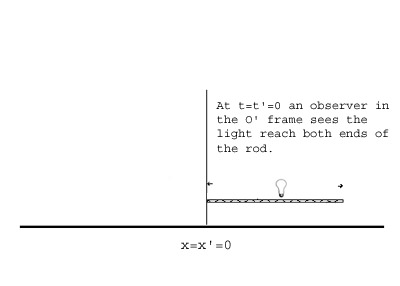How long does this light travel in the O frame? Ans: L/2(1 - v). The flash arrives at the left end of the rod at time t=0, so the difference in arrival times equals its arrival time at the right end of the rod. That is, it arrives at the right end of the rod at
t = L/2(1 - v) - L/2(1 + v) = Lv/(1 - v²) = Lvγ²
What is the position of the right end of the rod when the light arrives? The x coordinate of the rod at time t=0 is L, and its moving to the right with velocity v, so when the flash arrives its position is given by
x = L + vLv / (1 - v²) = L(1 - v² + v²) / (1 - v²) = L γ²
So, the point (0, L')' in O' coordinates corresponds to (Lvγ², L γ²) in O coordinates. Since L = L'/ γ, this can be written (L'vγ, L' γ)

From the above it can be seen that the equation for the t' = 0 line is t = vx in O coordinates. The events on this line are simultaneous in the O' frame with the event at the origin (0', 0') in O' coordinates. This is the O' now line for t' = 0.

Summarizing, the O frame coordinates of (0, L')' are (L'vγ, L' γ), and the equation of the t' = 0 line is t = vx.

Drawing Space-time Diagrams Showing the Lorentz Coordinate Transformation

The Lorentz Coordinate Tranformation incorporates time dilation and length contraction. A space-time diagram showing the O and O' coordinates is shown. 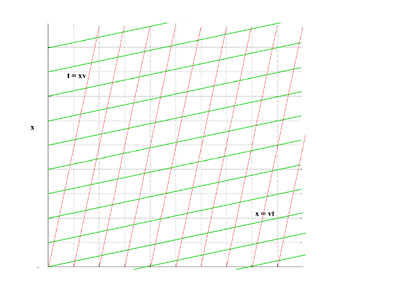It was drawn as follows:
- draw the worldline for the O' origin, that is, x = vt
- draw the now line for O' at t' = 0, that is t = xv
- the spacing of the x' = 1, 2, 3 .. lines is given by L/γ (length contraction)
- the spacing of the t' = 1, 2, 3 .. lines is given by Tγ (time dilation)

A Mystery Solved

Now we can solve the mystery presented earlier. A flash goes off! 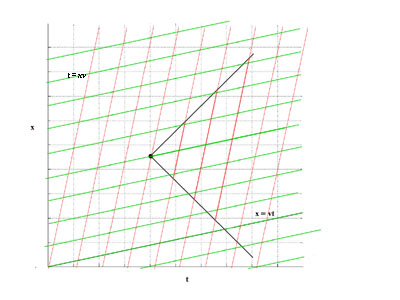With normalized scaling, the worldline of a photon of light is always at a 45 degree angle on a space time diagram. The event is marked with a dot on the diagram. Note that we're representing only one spacial dimension, so the flash of light is represented by two bursts of light, one traveling in plus x direction, and one in a negative x direction, the worldlines of both bursts are shown.

The (horizontal) worldline of an observer in frame O that was at the spot where the flash occurred is shown in the diagram. 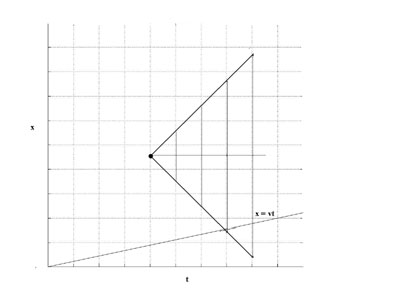The vertical now lines for the observer are also shown. Note that the observer appears to be in the middle of the outward bound bursts of light.

The 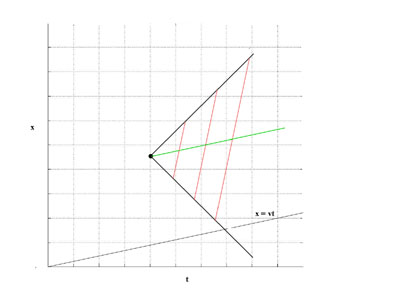(green) worldline of an observer in frame O' that was at the spot where the flash occurred is shown in the diagram. The (red) now lines for the observer are also shown. Note that at each instant, represented by a red line, the observer appears to be in the middle of the outward bound bursts of light. (!)

The Lorentz Transformation

Now we can write down the Lorentz Coordinate Transformation. We have the coordinates of an event (t', x', y', z')' in the O' frame and want to know its coordinates (t. x, y, z) in the O frame.

We have in O' frame coordinates (t', x')' = (0, x')' + (t', 0)'.

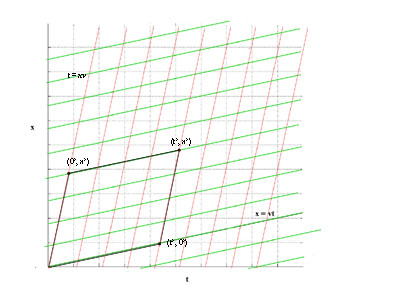
As we saw above, the O frame coordinates of (t', 0)' are ( t'γ, t'γv).

And, from the now line experiment the O frame coordinates of (0, x')' are (x'vγ, x' γ).

So we have
t = x'vγ + t'γ = (x'v + t')γ
x = vt'γ + x'γ = (vt' + x')γ
y = y'
z = z'

From F ≠ MA to E = Mc²

A train is moving with velocity v and an observer on the train throws a baseball forward with velocity u'. Common sense tells us that a stationary observer will see the ball travelling with velocity u = v + u'. This is the Galilean velocity transform. However, if the observer on the train shines a flashlight in the forward direction, the Michelson-Morely experiment tells us that both the observer on the train, and the stationary observer, will see the light travelling at velocity c (or 1 depending on scale). Well, c doesn't equal v + c, so the Galilean velocity transfrom isn't true for light. Physicists don't like to have one rule for one thing, and another rule for everything else, so the Galilean velocity transform was scrapped altogether and replaced with the Lorentz velocity transform which is true for baseballs and for light. We can derive it using the diagram above: if a ball is thrown from (0,0)' to (t', x')' with velocity u' = x'/t' in the O' frame, it's velocity in the O frame is given by

u = x/t = (vt' + x')γ / (x'v + t')γ = (vt' + x') / (x'v + t') = (vt' + u't') / (u't'v + t') = (v + u') / (u'v + 1)

Note that if v is very small, then the Lorentz velocity transform approximately equals the Galilean velocity transfrom; if u' = 1, then u = (v + 1) / (v + 1) = 1. A consequence of the Lorentz velocity transform is that no object can move at a velocity greater than 1 (or c in the usual scaling). We could differentiate both sides to get the Lorentz acceleration transfrom, but it's not necessary for our purposes, save to note that it's not a = a'.

But, now we have a problem, special relativity wreaks havoc with Newtonian physics, let's see why. The basis of Newtonian physics is F=MA; all the components, force (F), mass (M), and acceleration (A), are unaffected by the Galiliean coordinate transform, so F=MA is unchanged going from one inertial frame to another using the Galilean coordinate transform. However, acceleration is affected by the Lorentz coordinate transfrom. So, given that F and M are unaffected by change of observer, if F = MA in one frame, then since A changes with the observer, that is A' doesn't equal A, F will not equal MA' in the new oberver's frame.

So F = MA is not true for all inertial observers! In short, F ≠ MA. Physics was in a pickle. What to do?

Answer: well, F is expressed as a magnitude and direction, it can't vary with the observer, so, there is only one other option, that is to let mass m vary with the observer. A crazy idea, but it works! The concepts of work, momentum, and energy had been developed as part of Newtonian physics. The momentum of an object of mass m moving with velocity v is defined to be mv. Now, F=ma is equivalent to F = d(mv)/dt when mass is constant (as in Newtonian physics). If we allow for the possiblity that m is not constant, then this becomes

F = d(mv)/dt = dm/dt*v + m*dv/dt

From this alone, we can deduce E=Mc². When force accelerates an object energy is expended in the form of work, in Newtonian physics the energy reappears as an increase in the velocity of the object (the object's kinetic energy); in relativistic physics some of the energy reappears as an increase in the mass of the object, and some as an increase in the velocity of the object. Suppose we apply a force F for 1 second to an object travelling at velocity c, since the object's velocity cannot increase, all the energy will be transformed into an increase in mass. Let's do the math - the energy expended (E) equals the work which is the integral of force over distance, which is in this case F*c (the object travels a distance of c in one second), so E = Fc. Also,

F = d(mv)/dt = dm/dt*v + m*dv/dt = dm/dt*c + 0, so that dm/dt = F/c is constant for the second,

and the increase in mass (M) for the second is the integral of dm/dt over time which has the value F/c * 1, so that M = F/c = (E/c)/c, and E=Mc²

Magnetism is a Relativistic Phenomenon

Amazingly, special relativity explains magnetism. Consider a wire carrying a current as shown in the diagram. Imagine that the wire contains two streams, 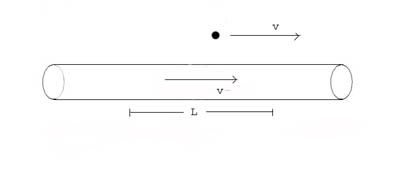one stream of electrons, and one stream of positively charged ions. If positive current is flowing to the left, the stream of electrons is moving to the right with velocity v as shown by the arrow. The stream of positive ions is stationary.

Consider a section of the wire of length L; let the number of electrons in this section of the wire be N, then the electron density (assume the wire cross section is 1 for simplicity) is N/L. A current carrying wire is electrically neutral, so the number of positive ions in this section is also N and the positive ion density is also N/L. Note that we have calculated these densities in the O frame of a stationary observer.

Imagine that there is an electron, outside the wire, that is also moving to the right with velocity v, and that this electron is at the origin of the O' frame. An observer in the O' frame also sees the electron stream and positive ion stream, however, for this observer, the positive ion stream is moving to the left with velocity -v and the electron stream is stationary.

The section of the positive ion steam observed to have length L (in the O frame) is contracted by γ when observed in the O' frame, hence its length in the O' frame is L_p' = L/γ, and the positive ion density calculated in the O' frame is N/L_p' = Nγ/L.

The electron stream is stationary in the O' frame, let Le' be the length measured in the O' frame of the section of the electron stream observed to have length L in the O frame. Since the electron stream is moving with velocity v in the O frame, L is equal to L_e'/γ due to length contraction. The electron density calculated in the O' frame is N/L_e' = N/(Lγ).

Since γ > 1, Nγ/L > N/(Lγ) and the wire is not elecrically neutral in the O' frame, and an observer in the O' frame sees an electrostatic force on the stationary electron. This force is perceived as magnetism in the O frame.

For the numbers, see, for example, "Fundamentals of Electricity and Magneticsm" by Arthur F. Kip, McGraw-Hill.