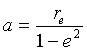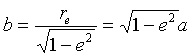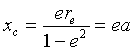Calculus Without Tears
Planetary Motion and the Two-Body Problem
Introduction
In the latter half of the seventeenth century, Issac Newton solved the two-body problem and explained the motion of objects in the sky, solving a mystery that had haunted mankind from the beginning. How important was this? In the history of the intellectual development of the human race the first big step was when we came down out of the trees, the second was Newton's solution to the two-body problem, we're waiting for the third.
Newton discovered gravity, discovered the laws of motion, developed calculus, and yet the hard work still lay before him. His goal was to explain the motion of objects in the sky. Kepler had proposed three laws of planetary motion, and had recorded a great amount of data that suggested that the laws did describe the motion of the planets in particular. However, Kepler had no idea why his laws held. Newton's goal was to explain Kepler's laws. He succeeded, and his efforts mark the beginnings of modern mathematics and physics. It's the most significant event in the history of our understanding of how the world works.
And yet, here's a little bet for you, I'll bet that you cannot find a solution to the two-body problem in any book that is being used in any high school or university undergraduate course in math, physics, or engineering. Email me if I'm wrong.
Note: the one-dimensional case is covered here.
Simplified Planetary Motion
We will start by making a good assumption, that the sun and an orbiting planet can be represented by point masses, and that the force between them is given by Newton's law of gravity. We will also make an assumption that is not true, that the sun is 'fixed' in space and does not move. This second assumption simplifies the problem; after solving the simplified problem in this section, we will drop the assumption in the next section and solve the problem without it.
Polar Coordinates
The sun will be fixed at the origin of the coordinate frame. We will use polar coordinates to describe the planet's trajectory, r(t) and θ(t).
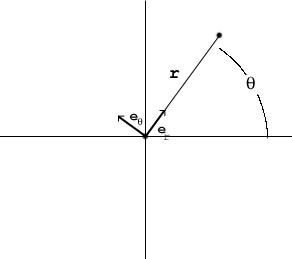
Define two unit (having length 1) vectors, er pointing from the origin to the planet,
er = (cos(θ), sin(&theta))
and the vector eθ rotated 90 deg. counter-clockwise from er,
eθ = (-sin(θ), cos(&theta))
The planet's position is given by
r(t) = r(t)er = r(t)(cos(θ), sin(&theta))
Note: vectors are in bold type, so r(t) is the vector from the origin to the planet, and r(t) is the length of the vector.
Note that
er'(t) = (cos(θ(t)), sin(θ(t))' = θ'(t)(-sin(θ(t), cos(θ(t)) = θ'(t)eθ
and
eθ'(t) = (-sin(θ(t)), cos(θ(t))' = θ'(t)(-cos(θ(t), -sin(θ(t)) = -θ'(t)er
The planet's velocity is given by
v(t) = r'(t) = r'(t)er(t) + r(t)er'(t) = r'(t)er + r(t)θ'(t)eθ
The planet's acceleration is given by
a(t) = v'(t) = r'(t)er'(t) + r''(t)er + r(t)θ'(t)eθ'(t) + (r(t)θ''(t) + r'(t)θ'(t))eθ
thus
a(t) = r'(t)θ'(t)eθ + r''(t)er - r(t)θ'(t)θ'(t)er + (r(t)θ''(t) + r'(t)θ'(t))eθ
and
a(t) = (r''(t) - r(t)θ'(t)2)er + (r(t)θ''(t) + 2r'(t)θ'(t))eθ
The Differential Equations of Motion
Now we'll use Newton's Law of Motion to write
F(t) = ma(t)
Where F is the force acting on the planet and m is the mass of the planet. We are assuming that the only force acting on the planet is due to gravity, and using Newton's Law of Gravity, we have
GMm/r(t)2 = ma(t)
where M is the mass of the earth and G is the gravitational constant. The direction of the gravitational force is -er, so we have
a(t) = -GM/r(t)2er
From the above, we have two equations of motion,
r''(t) - r(t)θ'(t)2 = -GM/r(t)2
and since the eθ component of a is 0,
r(t)θ''(t) + 2r'(t)θ'(t) = 0
Solving the Equations of Motion
We'd like to be able to solve the DEs and write down the functions of time that describe the planet's orbit. That ain't happening. We have two coupled differential equation; one is non-linear. Non-linear equations are difficult; none of the techniques we've studied in CWT Vols 1 thru 4 apply to this problem. No analytic solution exists. Imagine Newton, after discovering gravity, the laws of motion, and calculus, finally writing down his first differential equation, and it's not solvable. Tough break! The problem of calculating the trajectory as a function of time is known as Kepler's problem, and it can be solved iteratively, see the reference at the bottom of the page.
While a closed form solution is not possible, Newton was able to show that Kepler's laws could be derived from the equations of motion. We will content ourselves with showing that the orbit is an ellipse.
Multiplying the second equation of motion by r(t) gives
r(t)2θ''(t) + 2r(t)r'(t)θ'(t) = 0
The left hand side of the equation is (r(t)2θ'(t))', so we have
(r(t)2θ'(t))' = 0
and hence
r(t)2θ'(t) = h, a constant.
r(t)θ'(t) is the tangential velocity of the planet, and mr(t)r(t)θ'(t) is the angular momentum of the planet. So this shows that the angular momentum of the planet is constant, corresponding to Kepler's second law.
At this point, things get tricky :) . We want to determine r as a function of θ (call this function rθ), however the simpler relationship is between 1/r and θ so we begin with that and define
u(θ) = 1 / rθ(θ)
then (since r2(t)θ'(t) = h)
r'(t) = (1 / u(θ(t)))' = - u(&theta(t))' / u(&theta(t))2 = -r(t)2(du/dθ)θ'(t) = -h(du/dθ)
and
r''(t) = -h(d2u/dθ2)θ'(t) = -u2h2(d2u/dθ2)
The first equation can be re-written as (using θ'(t) = h / r2)
r''(t) - h2 / r3(t) = -GM / r2(t)
Then, substituting for r''(t), we have
-u2h2(d2u/dθ2) - u3h2 = -u2GM
and dividing by -u2h2 gives
(d2u/dθ2) + u = GM/h2
It is easily seen that the solution to the above DE is
u(θ) = GM/h2(1 - e cos(θ - θ0))
where e and θ0 are arbitrary constants. We have only one initial condition to match, u(0) = 1/rθ(0), so we can choose θ0 = 0 giving
rθ(θ) = (h2/GM)(1 / (1 - e cos(θ))
Et viola'. This shows that the planet's orbit is an ellipse (see last section).
The Two-Body Problem
Given that the preceeding was the simplified version of the problem, some trepidation in proceeding to the unsimplified version is understandable. However, not to fear, all the work has been done.
In reality, both the objects move. However, if no 'outside' forces are acting on the objects, their center of mass will be non-accelerating. We can use the center mass as the origin of the coordinates for the problem. Given these coordinates, a line from one object to the other will always pass through the origin.
Let r1 be the position vector of the 1st object, and r2 the position vector of the 2nd.
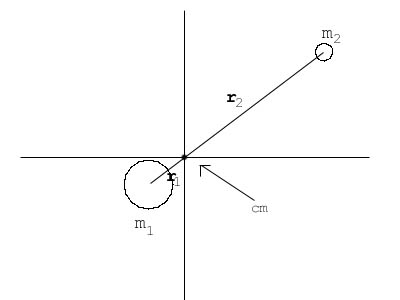 Then the center of mass is the point where
Then the center of mass is the point where
r1m1 = r2m2
Thus,
r = r1 + r2 = r1 + m1r1/m2
so
m2r = m2r1 + m1r1
and r = (m1 + m2)r1/m2
The magnitude of the gravitational force on m1 is
f = Gm1m2 / r2 = Gm1m2 / ((m1 + m2)r1/m2)2
so
f = Gm1m2 / r12 (m22/(m1 + m2)2)
Thus, since the gravitational force acts along the line between the objects, it is always directed to the origin. The magnitude of the gravitational force acting on m1 is less than (since r > r1)
f = Gm1m2/r12
So, by using the value m23 /(m1 + m2)2 for the mass of the 2nd object, the problem is identical to the one solved in the previous section.
Conic Sections and Polar Coordinates
The formula for an ellipse whose major axis is along the horizontal axis, in Cartesian coordinates, is
(x - xc2)/a2 + y2/b2 = 1
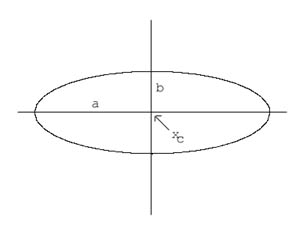
We will show that the formula for an ellipse in polar coordinates is
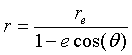
It's just a matter of going through the algebra. Multiplying:
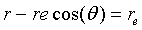
rcos(θ) = x, so
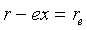
r = x2 + y2, so
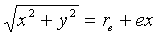
Squaring:
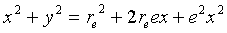
Rearranging:
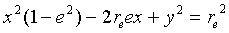
Dividing:
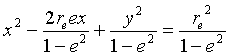
Completeing the square:

Rearranging and simplifying:
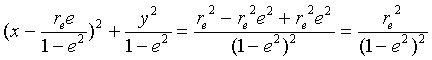
Et viola':
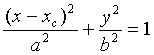
where e < 1 and: