Calculus Without Tears

General Relativity

Introduction

The next time you are at a basketball game, and a player launches a long shot from the backcourt, you might muse aloud "Ah, Einstein was correct, spacetime IS curved." If the fan next to you questions your judgement (or sanity), you can reply ... "See the arc of the ball, it is following the curvature of spacetime, just as described in Einstein's general theory of relativity", and, you would be exactly right. The photo shows Kareem Abdul Jabbar preparing to demonstrate Einstein's general theory. We'll calculate the radius of curvature of Kareem's sky hook in spacetime below, and the answer may surprise you.

Minkowski Spacetime, The Equations of Weingarten, Christoffel Symbols of the First and Second Kind, the Ricci Tensor, the Theorema Egregium, the Riemann Curvature Tensor, and more! Where special relativity didn't require any calculus, general relativity is a smorgasbord of differential equations.

General relativity is primarily a theory of why things fall, it replaces Newton's theory of gravity. According to the general theory as proposed by Einstein, the apple falls from the tree not because of some mysterious invisible force called gravity, but because the spacetime around the apple is curved by the large mass of the earth. How can we 'visualize' the new theory? ... actually, we don't have to visualize it as we can actually see it with our own two eyes. Remember, when Kareem releases his sky hook, there is no gravity pulling it down. So, why does it fall? Because spacetime is curved, and the ball is actually following a geodesic, or straight line, in curved spacetime. The arc of the ball's trajectory is due to the curvature of spacetime ..... there it is.

Riemannian Geometry

The mathematics of general relativity is the mathematics of non-Euclidean curved space, and, remarkably, the mathematics was invented before the advent of relativity, the mathematics of curved space was initiated by Gauss and further developed by his student, Riemann. Gauss was studying the problem of drawing a flat map of the earth, he discovered that a perfect distance preserving flat map couldn't be drawn because the earth is a curved surface. Note that a distance preserving flat map of a cylindrical surface can be drawn by unrolling the cylinder, thus, a cylinder is not a curved surface! Riemann added to the theory of curved surfaces and this branch of mathematics is called Riemannian geometry; there is no avoiding it if we are going to understand general relativity.

If what follows seems a little complex, be consoled to know that it is only 'elementary' Riemannian geometry. And, really, it's mostly just differentiating local basis vectors, expressing the result in the local frame, and giving names to the vector components. I.e., it mostly straightforward differentiation, combined with rearranging the terms and naming new functions. Much of the apparent compexity comes from the sheer number of functions, even for a two-dimensional curved surface this proliferation can be daunting. Note that every one-dimensional curve has a straight line distance preserving map, and so we can't simplify matters further by reducing the dimension to one as there are no one-dimensional curved spaces.

Curves in Euclidean 3-Space

A curve in E³ is given by a vector valued function
a(t) = (x(t), y(t), z(t))
the velocity of the curve is
a'(t) = (x'(t), y'(t), z'(t))
and the acceleration is
a''(t) = (x''(t), y''(t), z''(t))

A curve can be reparameterized with the parameter s which is the arc length of the curve, so that
length(a'(s)) = 1. When a curve is parameterized with its arc length, then the acceleration of the curve measures how fast the direction of the velocity of the curve is changing, and the curvature of the curve is defined to be length(a''(s))

Example:
the curve a(s) = (R*sin(s/R), R*cos(s/R), 0) is a circle in the x-y plane with radius R. It is parameterized by arc length.
a'(s) = ((1/R)R*cos(s/R), -(1/R)R*sin(s/R), 0) and length(a'(s)) = 1, and,
a''(s) = (-(1/R)²R*sin(s/R), -(1/R)²R*cos(s/R), 0) and length(a''(s)) = 1/R

Thus, the curvature of a circle of radius R is 1/R. Seems right.

Curves in Surfaces in Euclidean 3-Space, 1st Derivative

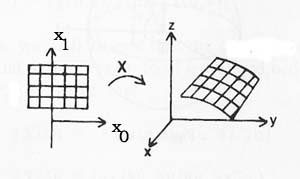We will define a 2-d surface in E³ as the image of a vector valued function from a region in E² to E³, eg,,
X(x₀,x₁) = (x(x₀,x₁), y(x₀,x₁), z(x₀,x₁))
With this definition, we get not only the surface itself, but also 2-d coordinates on the surface, with the coordinates of a point (a, b, c) on the surface equalling (x₀,x₁) where (a, b, c) = X(x₀,x₁)

A curve in the surface, parameterized by its arc length, is given by
a(s) = X(x₀(s), x₁(s))

We will spend a lot of time studying the 1st, 2nd, and 3rd derivatives of a curve. We begin: by the chain rule, the derivative of a' is given by
a'(s) = ∂X/∂x₀*x₀' + ∂X/∂x₁*x₁'
We use the notation X_i for ∂X/∂x_i
Then, the velocity vector of any curve at a point in the surface is a linear combination of X₀ and X₁, so, these vectors span a vector space, called the tangent vector space, at every point on the surface.

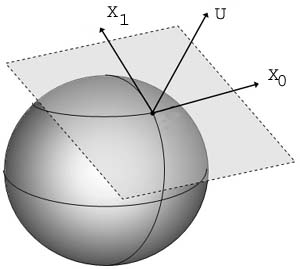We like for basis vectors to be orthogonal unit vectors, but, X₀ and X₁ may not be, so we define the symbols g_ij by g_ij = X_i · X_j , g_ij are the elements in a 2x2 matrix of 'metric coefficients' denoted by [g]. The importance of the metric coefficients is twofold, they can be computed by an inhabitant of the curved space, and they can be used to compute the curvature of the space, as we shall see. In Gauss's words - "These investigations deeply affect many other things, and I would go so far as to say that they are involved in the metaphysics of the geometry of space."

We'll need the following lemma later, it relates the dot product of a vector A with the basis vectors to the components of the vector:
If A = a₀X₀ + a₁X₁, and
b₀ = X₀·A = a₀g₀₀ + a₁g₀₁
b₁ = X₁·A = a₀g₁₀ + a₁g₁₁
then
[b_i] = [g][a_i] and [a_i] = [g]^-1[b_i]

Curves in Surfaces in Euclidean 3-Space, 2nd Derivatives and Gauss's Equations

The normal to the surface at a point is given by
U = X₀ x X₁ / abs(X₀ x X₁)

The 2nd derivative is, by the chain rule,
a' '(s) = x₀''*X₀ + x₀'*dX₀/ds + x₁''*X₁ + x₁'*dX₁/ds
dX₀/ds is evaluated along the curve, and we don't have an expression for it. We'll need a result from multi-variable calculus to analyze it further. Taylor's theorem for several variables (note: the one variable version is covered in CWT Vol. 3) can be used to show that
dX_i/ds = ∂X_i/∂x₀*x₀' + ∂X_i/∂x₁*x₁'

Now the fun can begin: with the notation ∂X_i/∂x_j = X_ij, note that X_ij is not necessarily in the tangent plane, so, we will separate it into its in plane and out of plane components, defining the functions G^r_ij , and L_ij, so that
X₀₀ = G⁰₀₀ X₀ + G¹₀₀ X₁ + L₀₀U
X₀₁ = G⁰₀₁ X₀ + G¹₀₁ X₁ + L₀₁U
X₁₀ = G⁰₁₀ X₀ + G¹₁₀ X₁ + L₁₀U
X₁₁ = G⁰₁₁ X₀ + G¹₁₁ X₁ + L₁₁U
These are Gauss's equations. Note that Gⁱ₁₀ = Gⁱ₀₁ and L₀₁ = L₁₀. Now we can write
a'' = (x₀'' + G⁰₀₀x₀'² + 2G⁰₀₁x₀'x₁' + G⁰₁₁x₁'²)X₀ +
(x₁'' + G¹₀₀x₀'² + 2G¹₀₁x₀'x₁' + G¹₁₁x₁'²)X₁ +
(L₀₀x₀² + 2L₀₁x₀x₁ + L₁₁x₁²)U

The Christoffel Symbols

The G^r_ij symbols above are called Christoffel symbols of the second kind. We also have Christoffel symbols of the first kind defined by G_ijk = X_ij·X_k. The following 'three card monte' shows that the Christoffel symbols are functions of the metric coefficients; we will make use of this computing a solution to the field equations below: Differentiating
∂g_ik/∂x_j = ∂(X_i·X_k)/∂x_j = X_ij·X_k + X_kj·X_i = G_ijk + G_kji
Permutting indices yields
∂g_kj/∂x_i = G_kij + G_jik
and,
∂g_ji/∂x_k = G_jki + G_ikj
Subtracting the third equation from the sum of the first two gives
G_ijk = (1/2)*(∂g_ik/∂x_j + ∂g_jk/∂x_i - ∂g_ij/∂x_k)
and by the lemma above
[Gⁱ_jk] = [g]^-1[G_ijk]

The Equations of Weingarten

Since U · U = 1, the partial derivatives of U, denoted by U_i, are in the tangent plane and can be written, defining the functions Lⁱ_j, as U_i = L⁰_iX₀ + L¹_iX₁. These are the equations of Weingarten.

Since U · X_j = 0, differentiating both sides wrt x_k gives
U · X_jk + U_k · X_j = 0, so that
U_k · X_j = - U · X_jk = -L_jk
And, from the lemma,
[-L_ij] = [g] [Lⁱ_j] so that [Lⁱ_j] = [g]^-1[-L_ij]

The Riemann-Christofel Curvature Tensor

Hang in there, we've almost arrived. We will differentiate Gauss's equations with the goal of developing some equations for the second derivatives. Differentiating

X_ij = G⁰_ij X₀ + G¹_ik X₁ + L_ijU
wrt x_k gives
X_ijk = dG⁰_ij/∂x_kX_ij + G⁰_ijX_0k + dG¹_ij/∂x_kX₁ + G¹_ijX_1k + L_ijkU + L_ijU_k

Using Gauss's equations to write X_rkas a linear combination of X₀ , X₁ and U, and Weingarten's equations to write U_k as a linear combination of X₀ and X₁, and rearranging the terms gives
X_ijk = (∂G⁰_ij/∂x_k + G⁰_ijG⁰_0k + G¹_ijG⁰_1k - L_ijL⁰_k)X₀ + (dG¹_ij/∂x_k + G⁰_ijG⁰_0k + G¹_ijG¹_1k - L_ijL¹_k)X₁ + (.......)U
Exchanging j and k gives
X_ikj = (∂G⁰_ik/∂x_j + G⁰_ikG⁰_0j + G¹_ikG⁰_1j - L_ikL⁰_j)X₀ + (dG¹_ik/∂x_j + G⁰_ikG⁰_0j + G¹_ikG¹_1j - L_ikL¹_j)X₁ + (.......)U

Since X_ijk = X_ikj, subtracting the 1st equation from the 2nd gives
0 = ∂G⁰_ik/∂x_j - dG⁰_ij/∂x_k + G⁰_ikG⁰_0j + G¹_ikG⁰_1j - G⁰_ijG⁰_0k - G¹_ijG⁰_1k - L_ijL⁰_k + L_ikL⁰_j
and
0 = ∂G¹_ik/∂x_j - dG¹_ij/∂x_k + G⁰_ikG¹_0j + G¹_ikG¹_1j - G⁰_ijG¹_0k - G¹_ijG¹_1k - L_ijL¹_k + L_ikL¹_j

Defining R^h_ijk = ∂G^h_ik/∂x_j - ∂G^h_ij/∂x_k + G⁰_ikG^h_0j + G¹_ikG^h_1j - G⁰_ijG^h_0k - G¹_ijG^h_1k
we have
R^h_ijk = L_ikL^h_j - L_ijL^h_k

The R^h_ijk are the components of the Riemann curvature tensor. Note that the Riemann curvature tensor is defined in terms of the Christoffel symbols, which are functions of the metric coefficients. The L_ij and Lⁱ_j are functions of how the normal vector U changes, i.e., the curvature of the surface. Gauss defined the curvature of a 2-d surface geometrically, and showed that it equals det([L])/det([g]). The Riemann curvature tensor allows the curvature to be computed from values that can be calculated in the surface, the g_ij. It provides the building blocks for the left side of Einstein's field equations.

The Ricci Tensor and Einstein's Field Equations

It's time to get down to business. As is our wont, we will simplify things as much as possible by considering a 1-d world, giving 2-d spacetime. Einstein's field equations for empty space are
R_ij = 0
where R_ij = R⁰_ij0 + R¹_ij1
The R_ij are the components of the Ricci tensor.

Our goal now is to solve these equations for a world containing a single point mass M surrounded by a vacuum. The 16 components of the Riemann curvature tensor are:
R⁰₀₀₀ = ∂G⁰₀₀/∂x₀ - ∂G⁰₀₀/∂x₀ + G⁰₀₀ G⁰₀₀ + G¹₀₀ G⁰₁₀ - G⁰₀₀ G⁰₀₀ - G¹₀₀ G⁰₁₀ (= 0)
R¹₀₀₀ = ∂G¹₀₀/∂x₀ - ∂G¹₀₀/∂x₀ + G⁰₀₀ G¹₀₀ + G¹₁₀ G⁰₁₀ - G⁰₀₀ G¹₀₀ - G¹₀₀ G¹₁₀ (= 0)
R⁰₁₀₀ = ∂G⁰₁₀/∂x₀ - ∂G⁰₁₀/∂x₀ + G⁰₁₀ G⁰₀₀ + G¹₁₀ G⁰₁₀ - G⁰₁₀ G⁰₀₀ - G¹₁₀ G⁰₁₀ (= 0)
R¹₁₀₀ = ∂G¹₁₀/∂x₀ - ∂G¹₁₀/∂x₀ + G⁰₁₀ G¹₀₀ + G¹₁₀ G¹₁₀ - G⁰₁₀ G¹₀₀ - G¹₁₀ G¹₁₀ (= 0)
R⁰₀₁₀ = ∂G⁰₀₀/∂x₁ - ∂G⁰₀₁/∂x₀ + G⁰₀₀ G⁰₀₁ + G¹₀₀ G⁰₁₁ - G⁰₀₁ G⁰₀₀ - G¹₀₁ G⁰₁₀
R¹₀₁₀ = ∂G¹₀₀/∂x₁ - ∂G¹₀₁/∂x₀ + G⁰₀₀ G¹₀₁ + G¹₁₀ G⁰₁₁ - G⁰₀₁ G¹₀₀ - G¹₀₁ G¹₁₀
R⁰₁₁₀ = ∂G⁰₁₀/∂x₁ - ∂G⁰₁₁/∂x₀ + G⁰₁₀ G⁰₀₁ + G¹₁₀ G⁰₁₁ - G⁰₁₁ G⁰₀₀ - G¹₁₁ G⁰₁₀
R¹₁₁₀ = ∂G¹₁₀/∂x₁ - ∂G¹₁₁/∂x₀ + G⁰₁₀ G¹₀₁ + G¹₁₀ G¹₁₁ - G⁰₁₁ G¹₀₀ - G¹₁₁ G¹₁₀
R⁰₀₀₁ = ∂G⁰₀₁/∂x₀ - ∂G⁰₀₀/∂x₁ + G⁰₀₁ G⁰₀₀ + G¹₀₁ G⁰₁₀ - G⁰₀₀ G⁰₀₁ - G¹₀₀ G⁰₁₁
R¹₀₀₁ = ∂G¹₀₁/∂x₀ - ∂G¹₀₀/∂x₁ + G⁰₀₁ G¹₀₀ + G¹₁₁ G⁰₁₀ - G⁰₀₀ G¹₀₁ - G¹₀₀ G¹₁₁
R⁰₁₀₁ = ∂G⁰₁₁/∂x₀ - ∂G⁰₁₀/∂x₁ + G⁰₁₁ G⁰₀₀ + G¹₁₁ G⁰₁₀ - G⁰₁₀ G⁰₀₁ - G¹₁₀ G⁰₁₁
R¹₁₀₁ = ∂G¹₁₁/∂x₀ - ∂G¹₁₀/∂x₁ + G⁰₁₁ G¹₀₀ + G¹₁₁ G¹₁₀ - G⁰₁₀ G¹₀₀₁ - G¹₁₀ G¹₁₁
R⁰₀₁₁ = ∂G⁰₀₁/∂x₁ - ∂G⁰₀₁/∂x₁ + G⁰₀₁ G⁰₀₁ + G¹₀₁ G⁰₁₁ - G⁰₀₁ G⁰₀₁ - G¹₀₁ G⁰₁₁ (= 0)
R¹₀₁₁ = ∂G¹₀₁/∂x₁ - ∂G¹₀₁/∂x₁ + G⁰₀₁ G¹₀₁ + G¹₁₁ G⁰₁₁ - G⁰₀₁ G¹₀₁ - G¹₀₁ G¹₁₁ (= 0)
R⁰₁₁₁ = ∂G⁰₁₁/∂x₁ - ∂G⁰₁₁/∂x₁ + G⁰₁₁ G⁰₀₁ + G¹₁₁ G⁰₁₁ - G⁰₁₁ G⁰₀₁ - G¹₁₁ G⁰₁₁ (= 0)
R¹₁₁₀ = ∂G¹₁₁/∂x₁ - ∂G¹₁₁/∂x₁ + G⁰₁₁ G¹₀₁ + G¹₁₁ G¹₁₁ - G⁰₁₁ G¹₀₁ - G¹₁₁ G¹₁₁ (= 0)

Eight of the Riemann curvature tensor components are identically 0. The components of the Ricci tensor are
R₀₀ = R⁰₀₀₀ + R¹₀₀₁ = R¹₀₀₁
R₀₁ = R⁰₀₁₀ + R¹₀₁₁ = R⁰₀₁₀
R₁₀ = R⁰₁₀₀ + R¹₁₀₁ = R¹₁₀₁
R₁₁ = R⁰₁₁₀ + R¹₁₁₁ = R⁰₁₁₀

Solving the Equations

A few weeks after Einstein published the general theory in 1915, he received a letter from Karl Schwarzchild , a German astrophysicist, who was fighting on the Russian front. The letter contained a solution to the field equations for a single point mass located in empty space. This solution is now known as the Schwarzchild solution. We can simplify it by considering a space of only 1 dimension, and the resulting spacetime with 2 dimensions.

We assume that the coordinates are orthogonal, so that g₀₁ = g₁₀ = 0; and we define functions m and n so that g₀₀ = e^m and g₁₁ = -eⁿ. The formula for the Christoffel symbols becomes
Gⁱ_jk = 1/(2g_ii)(∂g_ji/∂x_k + ∂g_ki/∂x_j - ∂g_kj/∂x_i)
giving
G⁰₀₁ = G⁰₁₀ = 1/(2g₀₀)(∂g₀₁/∂x₀ + ∂g₀₀/∂x₁ - ∂g₀₁/∂x₀) = 1/(2g₀₀)(∂g₀₀/∂x₁) = m'
G¹₀₀ = 1/(2g₁₁)(∂g₁₀/∂x₀ + ∂g₀₁/∂x₀ - ∂g₀₀/∂x₁) = 1/(2g₁₁)( - ∂g₀₀/∂x₁) = - m'e^{2m - 2n}
G¹₁₁ = 1/(2g₁₁)(∂g₁₁/∂x₁ + ∂g₁₁/∂x₁ - ∂g₁₁/∂x₁) = 1/(2g₁₁)(∂g₁₁/∂x₁) = n'
G⁰₀₀ = G⁰₁₁ = G¹₀₁ = G¹₁₀ = 0

The 1st field equation is
0 = R₀₀ = R¹₀₀₁ = ∂G¹₀₁/dt - ∂G¹₀₀/∂x + G⁰₀₁ G¹₀₀ + G¹₀₁ G⁰₁₀ - G⁰₀₀ G¹₀₁ - G¹₀₀ G¹₁₁
that is,
0 = 0 + d( - m'e^{2m - 2n})/∂x + m'm'e^{2m - 2n} + 0*0 - 0*0 + n'm'e^{2m - 2n}
0 = (- m'' + n'm' - m'²)e^{2m - 2n}
and R₀₁ and R₁₀ are identically 0, and R₁₁ is equivalent to the 1st.

The differential equation
- m'' + n'm' - m'² = 0 is solved by inspection by m = (1/2)ln(a + bx), n = -(1/2)ln(a + bx)
so the solution is g₀₀ = a + bx, g₀₁ = g₁₀ = 0 and g₁₁ = -1/(a+bx)

Geodesics and the Curvature of Spacetime

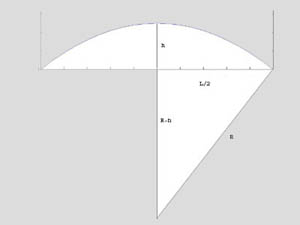Let's compute the radius of curvature for Kareem's hook shot. In 1-d space, he'll have to shoot the ball straight up and then it will fall straight down. Suppose it is launched upward with a velocity of 10 m/sec, so it will travel upward for one second, reaching a height of 5m, and then descend for one second. Note that we will compute the arc of the ball's worldline in spacetime, not the 'frozen' arc of the ball in space only. The worldline arc is plotted to the right, but, not to scale. Note that the t axis units are seconds (time), and the x axis units are centimeters (distance). To use the same units on both axes, we need to convert to common 'geometric units' by convereting the time units to distance, and the conversion factor is c, the speed of light (3x10¹⁰ cm/sec). Thus, if drawn to scale, the horizontal axis would be 2*3x10¹⁰ units long. The arc should be beginning to look more straight now. We can compute the approximate radius of curvature: the arc is a parabola, but we will approximate it by a circle. We have
(R - h)² + (L/2)² = R² and R = (h² + (L/2)²)/2h
setting L = 2*3x10¹⁰ and h = 500 gives a curvature of (1/R) = 7.5*10^-18

The gravitational acceleration for an earth like mass is -980 cm/sec² = -G = -10/c*c = -10^-20

In flat spacetime, a straight line is a straight line, in curved spacetime, a straight line is a line whose curvature is solely due to the curvatue of spacetime, such a curve is called a geodesic. Recall the formula for the second derivative of a curve in a surface,
a'' = (x₀'' + G⁰₀₀x₀'² + 2G⁰₀₁x₀'x₁' + G⁰₁₁x₁'²)X₀ +
(x₁'' + G¹₀₀x₀'² + 2G¹₀₁x₀'x₁' + G¹₁₁x₁'²)X₁ +
(L₀₀x₀² + 2L₀₁x₀x₁ + L₁₁x₁²)U

The curvature in the surface is represented by the in plane components of a''; thus a curve is a geodesic if and only if
x₀'' = - (G⁰₀₀x₀'² + 2G⁰₀₁x₀'x₁' + G⁰₁₁x₁'²)
and
x₁'' = - (G¹₀₀x₀'² + 2G¹₀₁x₀'x₁' + G¹₁₁x₁'²)

We will substitute t for x₀ and x for x₁. The ' above represents differentiation wrt arc length, and, since ∂x << dt, we can omit the terms on the right side of the equations involving x', thus we have for a geodesic, with a = 1 and b = 2G
t'' = - G⁰₀₀t'² = 0
x'' = - G¹₀₀t'² = -(-1/2g₁₁)∂g₀₀∂x = (1/2g₁₁)(2G) = -G

From the first equation, t'' is 0 so that t is a constant multiple of arc length; the constant is very close to 1 since the arc length and change in t are nearly the same, thus approximately t' = 1. From the second equation, approximating g₁₁ with -1, we have ∂x²/dt² = -G, thus we have arrived at a DE for the trajectory of the ball, that is
∂x²/dt² = -G
and this is similar to the Newtonian result.

Note that the downward acceleration of the ball does not depend on the ball's position, in contrast to gravity as we know it where the acceleration increases as the ball falls due to the increasing strength of gravity. The reason is the following: in 3-d, as the distance from a mass increases the gravitational force decreases in such a way that when integrated over a ball of radius r, the result is a constant. Thus, the force decreases proportional to 1/r². In a 2-d world the gravitational force decreases proportional to 1/r. In a 1-d world it doesn't decrease.

References

Richard L. Faber, "Differential Geometry and Relativity Theory", Marcel Dekker, 1983